In today's digital age, character recognition has become an important aspect of data processing. Whether it's recognizing handwritten text, printed text, or special characters, character recognition is an essential AI tool that can help automate many processes, saving time and effort. This is where Recognition comes in. It's an app that utilizes self-learning algorithms to accurately recognize a wide variety of characters. The aim of this article is to delve into the technical aspects of the Recognition application, demonstrating key points with relevant examples.

About the Application
Recognition is a mobile application that utilizes machine learning to recognize various characters. The application is designed more to demonstrate the capabilities of machine learning, and not for everyday use, but this does not make it less interesting, but rather the opposite.
Recognition is an app that uses advanced machine learning algorithms, specifically a type of algorithm called a perceptron, to recognize various characters. Once the character is uploaded, Recognition processes it through its self-learning algorithm, which is trained to recognize different types of characters. The more often the user interacts with the application, the more accurate the algorithm becomes, since it constantly learns from the processed data.
How the Recognition App Works
This section will describe the working mechanisms of Recognition.
First, let's discuss some terminology.
Neuron
Neuron is a computing unit that receives information. Within such a unit, some mathematical calculations are performed on the input data, after which the data is transmitted either to the next neuron in the “chain” or to the output of the neural network. Relatively speaking, a neuron is a “box” with several inputs (their number depends on the type of input information, for example, we have a 24 by 24 pixel image, which means 24 * 24 = 576 inputs) and one output.
Axon
Axon – connection between neurons responsible for the transmission of signals from one neuron to another. Usually takes the form of a weighting factor that determines the importance of each connection between neurons. For us, these are the output values of neurons that transmit information to the next layer of the neural network.
Synapse
Synapse – a connection between neurons, responsible for modeling the interaction between neurons and determining the influence of each of them on the next one. Like an axon, a synapse is represented by a weight that determines the interaction between neurons. Specifically, in our case, the synapse is represented by weights between neurons, which determine the strength of the connection between them.
Weight
Weight – determines the importance of each input signal for calculating the output value of the neuron.
With the terminology clarified, we can now delve into the key functional features of the application. So, let's consider the main class, the concept of which is to collect the entire configuration of our Perceptron in one place.
class PerceptronConfig {
final List<String> alphabet;
int weightsNormalized;
int trainingIterations = 0;
int statsPeriod;
int inputsCount;
int outputsCount;
List<List<double>> weights;
List<int> errorsInStatsPeriod;
}The PerceptronConfig object contains information about the input data (an array of strings), the number of input and output neurons, the weight matrix, the array of error statistics in the learning process, and other parameters. This object will later be used to create and configure the Perceptron before it is trained and used in character recognition tasks.
It's fascinating to observe how a basic neural network struggles initially to recognize seemingly simple symbols. However, after a few iterations, it can accurately determine all possible variations of the input. Still, how does it work? Let's figure it out.
The first step involves obtaining a list of values for the output neurons. The list of output neurons will directly depend on the weights, which must be initialized with initial values if the model is launched for the first time and has never been trained yet. Typically, the weights are initialized randomly and given some distribution to ensure initial randomness and not get stuck in a local minimum of the loss function. The function below takes a list of values for input neurons and returns a list of values for output neurons – essentially the same axons.
List<double> _getOutputNeuronsValues(List<double> input) {
final List<double> outputNeurons = [];
for (int i = 0; i < outputsCount; i++) {
double sum = 0.0;
for (int j = 0; j < inputsCount; j++) {
sum += weights[i][j] * input[j];
}
outputNeurons.add(_getActivationFuncValue(sum));
}
return outputNeurons;
}Surely you noted the strange function _getActivationFuncValue, which has not yet been mentioned. Well, you need to figure it out. The Perceptron itself is a single layer neural network, hence it only has one layer of neurons that accept input values. Such neural networks are the simplest types of ANNs, that is, they are used for tasks that can be solved using a linear model, for example, as in our example, for classifying input data. In mathematical form, such a neural network can be represented as y = f(w * x + b), where x is the input data vector, w is the weight vector, b is the bias, and f is our _getActivationFuncValue function, which is also the activation function . The activation function in the Perceptron is a unit hop function in which the characteristic of the derivative is important. The derivative will not be defined at the point x = 0, therefore, often in the training of the Perceptron, gradient descent is used, so there is no need to calculate the derivative of the activation function.
This piece of text does not promise to be simple, but it is very important in the concept of training the Perceptron, so it is an inseparable part of this article.
double _getActivationFuncValue(double x) => 1 / (1 + exp(x));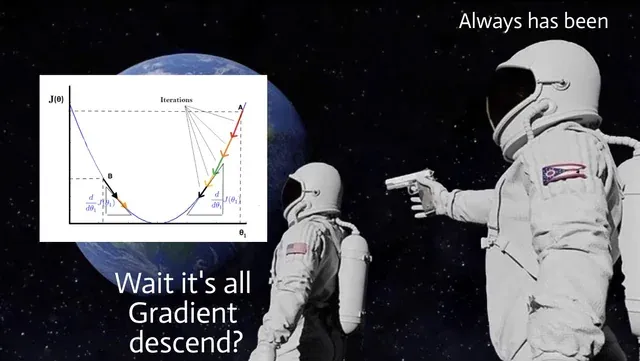
So, we have decided on obtaining output values at the output of each neuron, now we need to form the correct learning algorithm for our Perceptron. processInput method takes one required input parameter and optionally a correctIndex parameter.
int processInput(List<double> input, int? correctIndex)You are probably wondering what the input parameter is and where did it come from? This is our input data, namely a 24 by 24 pixel image (hence, each neuron will have 576 inputs), presented as a two-dimensional array, which the user sets himself by drawing the required symbol on the canvas. With these data we will train our Perceptron.
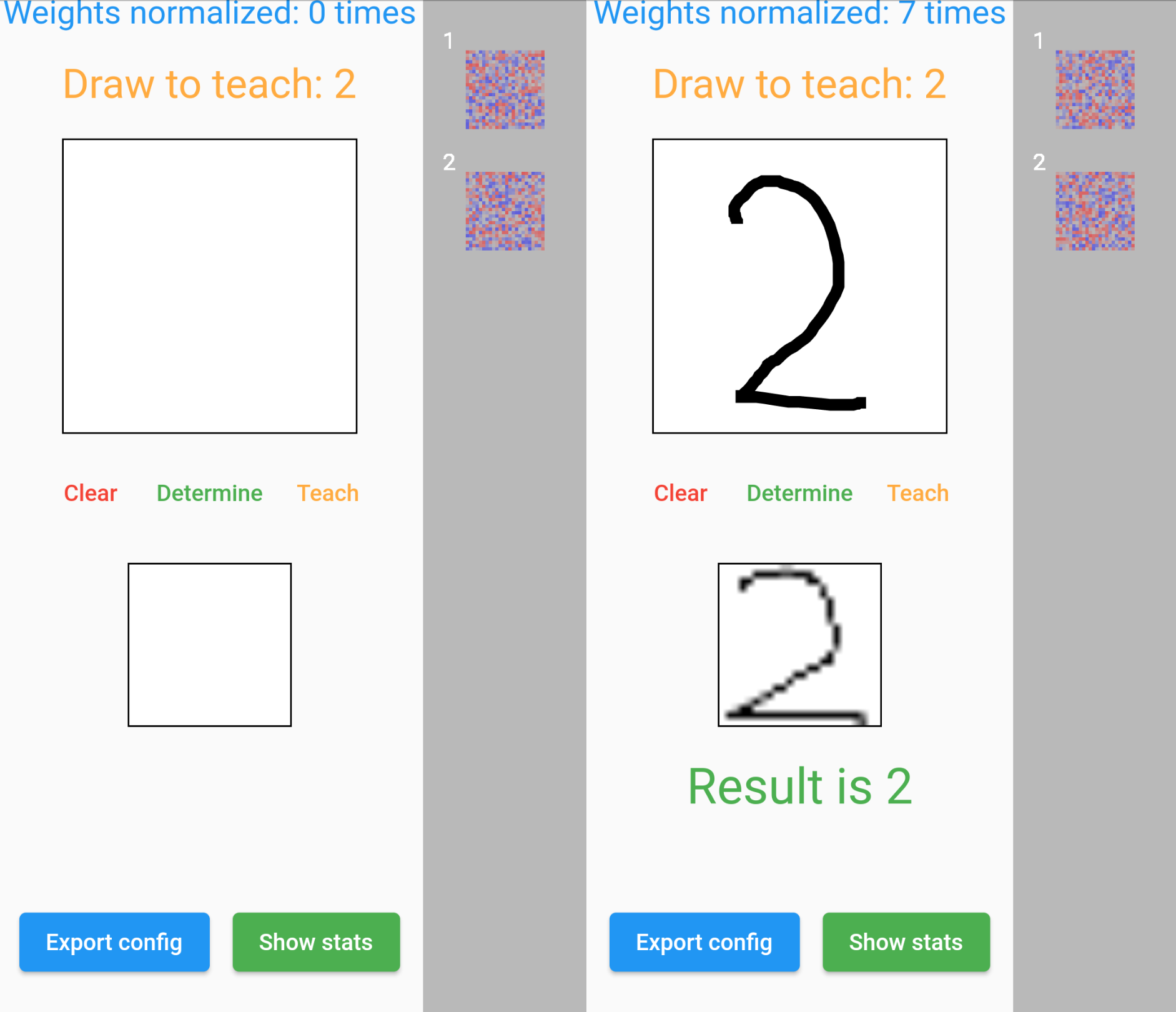
So let's move on. Taking a list of numbers input as input, we calculate the values of each output neuron using the previously written _getOutputNeuronsValues() function. Then we look for the index of the neuron with the maximum value, which will be used as the answer of the Perceptron.
final outputNeurons = _getOutputNeuronsValues(input);
final maxOutput = outputNeurons.reduce(max);
final outputIndex = outputNeurons.indexOf(maxOutput);The following correctIndex parameter is optional. If it is passed, then, in fact, this means that our neural network is in the process of learning and the weights should be adjusted for the output neuron that corresponds to the output neuron that has the largest weight value. As mentioned earlier, a neuron can have multiple inputs. Synapses connect this inputs to each such input, forming what looks like a one-way connection. Each synapse has its own significance, which is usually called weights.
If we go a little deeper into the case with a non-zero optional parameter, we can say that the method finds the expected value of the output neuron outputNeuronCorrect using correctIndex and checks whether the weights should be adjusted for this neuron or for other neurons. The weights are adjusted if the actual output value does not match the predefined value or if at least one of the output neurons has an output value greater than the specified _outputFittingCriterionvalue – the fit criterion for the output. If the output value of the neuron is less than this value then such an output cannot be considered correct.
static const double _outputFittingCriterion = 0.9;if (correctIndex != null) {
_config.trainingIterations++;
if (teachingIterations % statsPeriod == 1) {
/// Adding a new error counter each time in the beginning of a new period;
_config.errorsInStatsPeriod.add(0);
}
final outputNeuronCorrect = outputNeurons[correctIndex];
final correctOutputWeightsShouldBeCorrected = outputIndex != correctIndex ||
(outputIndex == correctIndex && maxOutput < _outputFittingCriterion);
final outputsNoCorrect = List.from(outputNeurons)..remove(outputNeuronCorrect);
final otherOutputsWeightsShouldBeCorrected = outputIndex != correctIndex ||
outputsNoCorrect.any((element) => element > _outputFittingCriterion);
if (correctOutputWeightsShouldBeCorrected) {
/// Adjusting weights leading to a predetermined correct output neuron;
final errorCorrect = 1 - outputNeuronCorrect;
/// The gradient is equal to the product of the error and the derivative of the activation
/// function. Since we use the logistic function: f'(x) = f(x)*(1 - f(x));
final localGradientCorrect =
max(errorCorrect * outputNeuronCorrect * (1 - outputNeuronCorrect), _minLocalGradient);
for (int i = 0; i < inputsCount; i++) {
weights[correctIndex][i] =
weights[correctIndex][i] - _convergenceStep * localGradientCorrect * input[i];
}
}
if (otherOutputsWeightsShouldBeCorrected) {
for (int i = 0; i < outputNeurons.length; i++) {
if ((i == outputIndex && outputIndex != correctIndex) ||
(i != correctIndex && outputNeurons[i] > _outputFittingCriterion)) {
final outputNeuron = outputNeurons[i];
final errorOutput = 0 - outputNeuron;
final localGradientOutput =
min(errorOutput * outputNeuron * (1 - outputNeuron), -_minLocalGradient);
for (int j = 0; j < inputsCount; j++) {
weights[i][j] = weights[i][j] - _convergenceStep * localGradientOutput * input[j];
}
}
}
}
if (correctOutputWeightsShouldBeCorrected || otherOutputsWeightsShouldBeCorrected) {
_config.errorsInStatsPeriod.last++;
_config.weightsNormalized++;
/// After adjusting the weights, we can't be sure that the perceptron will correctly process
/// the current input value, so it makes sense to recursively call [processInput] and adjust
/// the weights again. The recursive calls will continue until the perceptron correctly
/// processes the current input value;
///
/// The recursive call can be removed, but then it will take more time to train the network;
processInput(input, correctIndex);
}
}Ultimately, we get the index of the most activated neuron on the output layer, which corresponds to a certain data class. However, in the case when the perceptron made a mistake, that is, maxOutput is less than the set exit criterion in _outputFittingCriterion, we will get a negative index.
return maxOutput >= _outputFittingCriterion ? outputIndex : -outputIndex;I hope at this stage we have figured out how Recognition works under the hood. Of course, only the main part of the learning functionality of our Perceptron has been described, and some processes have remained behind the scenes, however, this part of the article does not aim to fully describe them, but only to provide background information for basic understanding.
Key Features of the Recognition App
- Self-learning algorithm: the machine learning algorithm of Recognition enhances its accuracy over time through user interactions.
- User-friendly interface: the intuitive interface makes the app easy to use for everyone.
- Multi-language support: Recognition recognizes characters in multiple languages, including Latin, Cyrillic, and Asian scripts.
- High accuracy: the advanced algorithm of Recognition ensures a high accuracy rate, correctly recognizing characters.
- Customizable: users can tailor the app's settings to improve accuracy or recognize specific types of characters.
Potential Use Cases for Recognition
Recognition has a wide range of potential use cases, such as:
- Translating handwritten notes into digital text
- Automatically reading and processing printed documents
- Recognizing special characters in scientific research
- Identifying characters in different languages for translation
- Assisting people with disabilities who have difficulty reading text
Conclusion
In conclusion, Recognition is a highly innovative character recognition app that employs advanced machine learning techniques to accurately discern various types of characters. With its self-learning algorithm and user-friendly interface, Recognition is a powerful tool that can save time and effort in various data processing tasks. If you're interested in developing similar applications or exploring more about Flutter, check out our flutter app development services. Whether you're a student, a researcher, or a professional, Recognition can help make your work easier and more efficient. Try out Recognition today and experience the power of self-learning character recognition!











